scikit-learnは機械学習を含むデータマイニングやデータ解析のライブラリです。
pythonで深層学習以外の機械学習を実行するツールキットとししてデファクトスタンダードとなっています。
前処理
機械学習のアルゴリズムを適用する前に、データの特性を理解して前処理を行うことが重要です。
前処理はデータ解析の8割から9割を占めるともいわれる大変重要な工程です。
欠損値への対応
欠損値はそのままにするとその後の解析が難しくなるため適切に対処する必要があります。
下記の2つの方法があります。
- 欠損値を除去する
- 欠損値を補完する
import numpy as np
import pandas as pd
#sampleデータセット
df=pd.DataFrame(
{
'A':[1,2,np.nan,4,5],
'B':[6,7,8,np.nan,10],
'C':[11,np.nan,13,14,15]
}
)
df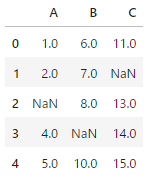
欠損値の除去
#欠損値かどうか確かめる
df.isnull()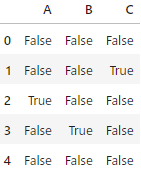
欠損値の補完
欠損値の補完とは、欠損値にある値を代入する処理です。
代入する値には特徴量の平均値、中央値、最頻値などがあります。
欠損値の補完は、pandasのDataFrameのfillnaメソッド、scikit-learnのpreprocessiongモジュールのImputerクラスを使用して行います。
strategy引数は、mean(平均値)、median(中央値)、most_frequent(最頻値)のいずれかを選択できます。
from sklearn.impute import SimpleImputer
#平均値を補完
imp=SimpleImputer(strategy='mean')
#欠損値を補完
imp.fit(df)
imp.transform(df)
カテゴリ変数のエンコーディング
カテゴリ変数とは、いくつかの限られた値においてどれに該当しているかを示す変数です。
import pandas as pd
df = pd.DataFrame(
{
'A':[1,2,3,4,5],
'B':['a','c','a','c','b']
}
)
df
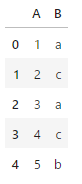
機械学習ではカテゴリ変数を扱う場合、コンピュータが処理しやすいように数値に変換する必要があります。
- カテゴリ変数のエンコーディング
- One-hotエンコーディング
カテゴリ変数のエンコーディング
カテゴリ変数のエンコーディングとは「a→0、b→1、c→2」のようにカテゴリ変数を数値(整数)に変換する処理を指します。
from sklearn.preprocessing import LabelEncoder
#ラベルエンコーダのインスタンス生成
le=LabelEncoder()
#ラベルエンコーディング
le.fit(df['B'])
le.transform(df['B'])array([0, 2, 0, 2, 1])変換された値と元の値は、LabelEncocderのインスタンスのclasses_属性により確認できます。
le.classes_array(['a', 'b', 'c'], dtype=object)One-hotエンコーディング
One-hotエンコーディングとは、カテゴリ変数に対して行う符号化の処理です。
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.compose import ColumnTransformer
#DataFrameをコピー
df_ohe=df.copy()
#ラベルエンコーダのインスタンス化
le=LabelEncoder()
#a,b,cを1,2,3に変換
df_ohe['B']=le.fit_transform(df_ohe['B'])
#one-hotエンコーディングのインスタンス化
ohe=ColumnTransformer([("OneHotEncoder",OneHotEncoder(),[1])],remainder='passthrough')
#one-hotエンコーディング特徴量の正規化
特徴量の正規化とは、特徴量の大きさを揃える処理です。
分散正規化
分散正規化とは特徴量の平均が0、標準偏差が1となるように特徴量を変換する処理です。
ますはサンプルデータを生成します。
import pandas as pd
df = pd.DataFrame(
{
'A':[1,2,3,4,5],
'B':[100,200,300,400,500]
}
)
df 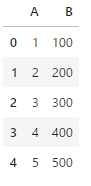
この作成したDataFrameに対して分散正規化を行います。
from sklearn.preprocessing import StandardScaler
#分散正規化のインスタンス生成
stdsc=StandardScaler()
#分散正規化を実行
stdsc.fit(df)
stdsc.transform(df)array([[-1.41421356, -1.41421356],
[-0.70710678, -0.70710678],
[ 0. , 0. ],
[ 0.70710678, 0.70710678],
[ 1.41421356, 1.41421356]])最小最大正規化
最小最大正規化は、特徴量の最小値が0、最大値が1をとるように特徴量を正規化する処理です。
from sklearn.preprocessing import MinMaxScaler
#最小最大正規化のインスタンス生成
mmsc=MinMaxScaler()
#最小最大正規化を実行
mmsc.fit(df)
mmsc.transform(df)array([[0. , 0. ],
[0.25, 0.25],
[0.5 , 0.5 ],
[0.75, 0.75],
[1. , 1. ]])分類
分類とは、データの「クラス」を予測して分けるタスクです。
回帰と並んで教師あり学習の典型的なタスクです。
下記の3つのアルゴリズムについてとりあげます。
- サポートベクターマシン
- 決定木
- ランダムフォレスト
分類モデル構築の流れ
分類モデルを構築するには、手元のデータセットを学習用とテスト用に分けます。そして学習データセットを用いて分類モデルを構築します。なお、学習用とテスト用に分けるのでなく、学習データセットとテストデータセットの分割を繰り返し、モデルの構築と評価を複数回行う方法は交差検証と呼ばれます。
scikit-learnのインターフェースでは、学習はfitメソッド、予測はpredictメソッドを用いて行います。
学習データセットとテストデータセットの準備
irisデータセットは花の種類が記録されたデータセットです。
from sklearn.datasets import load_iris
#Irisデータセットを読み込む
iris=load_iris()
x,y=iris.data,iris.target
#先頭3行を表示
print('x:')
print(x[:3,:])
print('y:')
print(y[:3])x:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]]
y:
[0 0 0]このデータを学習データとテストデータに分けるために、model_selectionモジュールのtrain_test_split関数を使用します。train_test_split(対象変数, test_size=テストデータの割合, random_state=データを分割する際のシード)
from sklearn.model_selection import train_test_split
#学習データとテストデータに分割
x_train, x_test, y_train, y_test=train_test_split(x,y, test_size=0.4, random_state=1230)
print(x_train.shape)
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)(90, 4)
(60, 4)
(90,)
(60,)サポートベクターマシン
サポートベクターマシンは、分類・回帰だけでなく外れ値検出にも使えるアルゴリズムです。
直線や平面などで分離できない(線形分離できない)データを高次元の空間に写して線形分離することにより、分類を行うアルゴリズムです。実際は、データ間の近さを定量化するカーネルを導入しています。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1230)
#X軸Y軸ともに0から1までの一様分布から100点をサンプリング
x0=np.random.uniform(size=(100,2))
#クラス0のラベルを100個生成
y0=np.repeat(0,100)
#x軸y軸ともに-1から0までの一様分布から100点をサンプリング
x1=np.random.uniform(-1.0,0.0,size=(100,2))
#クラス1のラベルを100個生成
y1=np.repeat(1,100)
#散布図にプロット
fig,ax=plt.subplots()
ax.scatter(x0[:,0],x0[:,1],marker='o',label='class0')
ax.scatter(x1[:,0],x1[:,1],marker='x',label='class1')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend()
plt.show()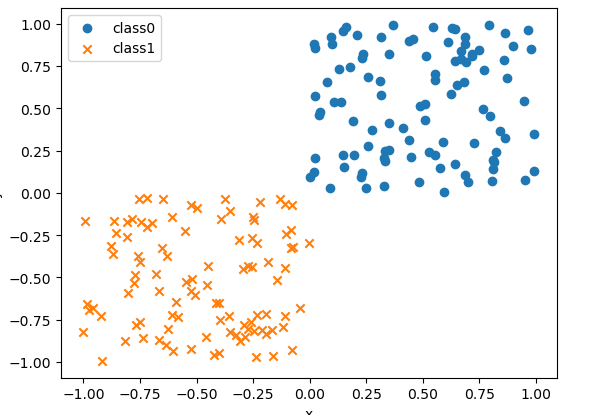
続いて、サポートベクターマシンによる学習を行います。
svmモジュールのSVCクラスをインスタンス化し、fitメソッドで学習します。
サポートベクターを可視化する処理は何度も使用するため、関数にまとめます。
この関数の引数Kernelにはサポートベクターマシンのカーネルを、引数CにはパラメータCを指定します。
from sklearn.svm import SVC
def plot_boundary_margin_sv(x0,y0,x1,y1,kernel,C,xmin=-1,xmax=1,ymin=-1,ymax=1):
#サポートベクターマシンのインスタンス化
svc=SVC(kernel=kernel,C=C)
#学習
svc.fit(np.vstack((x0,x1)),np.hstack((y0,y1)))
fig,ax=plt.subplots()
ax.scatter(x0[:,0],x0[:,1],marker='o',label='class0')
ax.scatter(x1[:,0],x1[:,1],marker='x',label='class1')
#決定境界とマージンをプロット
xx,yy=np.meshgrid(np.linspace(xmin,xmax,100),np.linspace(ymin,ymax,100))
xy=np.vstack([xx.ravel(),yy.ravel()]).T
p=svc.decision_function(xy).reshape((100,100))
ax.contour(xx,yy,p,
color='k',levels=[-1,0,1],
alpha=0.5,linestyles=['--','-','--'])
#サポートベクターをプロット
ax.scatter(svc.support_vectors_[:,0],
svc.support_vectors_[:,1],
s=250,facecolors='none',
edgecolors='aqua')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='best')
plt.show()#決定境界、マージン、サポートベクターをプロット
plot_boundary_margin_sv(x0,y0,x1,y1,kernel='linear',C=1e6) #Cの値は10の6乗
Cの値を大きくするとマージンが広くなります。
サポートベクタの数も増えます。
#決定境界、マージン、サポートベクターをプロット
plot_boundary_margin_sv(x0,y0,x1,y1,kernel='linear',C=0.1)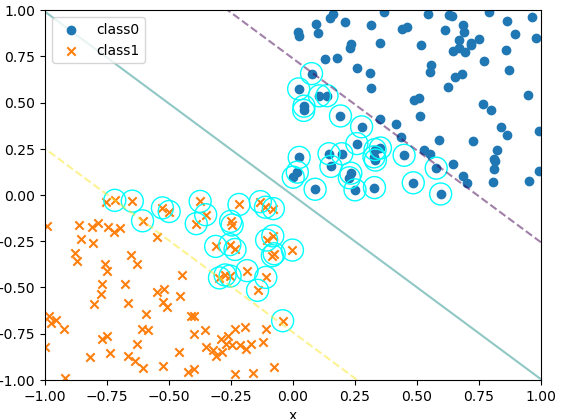
それでは次に直線で分離できないケースを見てみましょう。
下記はサンプルデータです。
np.random.seed(1230)
x=np.random.random(size=(100,2))
y=(x[:,1]>2*(x[:,0]-0.5)**2 + 0.5).astype(int)
fig,ax=plt.subplots()
ax.scatter(x[y==0,0],x[y==0,1],marker='o',label='class0')
ax.scatter(x[y==1,0],x[y==1,1],marker='x',label='class1')
ax.legend()
plt.show()
このデータに対してサポートベクターマシンでクラスを分類します。
kernel=’rbf’と指定することで、カーネルを動経基底関数を使用します。
x0,x1=x[y==0,:],x[y==1,:]
y0,y1=y[y==0],y[y==1]
plot_boundary_margin_sv(x0,y0,x1,y1,kernel='rbf',C=1e3,xmin=0,ymin=0)
決定木
決定木はデータを分割するルールを次々に作成していくことにより分類を実行するアルゴリズムです。
不純度の指標として、ジニ不純度、エントロピー、分類誤差などが用いられます。
ジニ不純度は,クラス分けをする時に,どれだけ綺麗に分けることができるかです。
つまり,分類した時にどれだけ「不純なもの」が含まれるかということです。
scikit-learnで決定木を実行するには、treeモジュールのDecisionTreeClassifierクラスを使用します。
DecisionTreeClassifierクラスのインスタンスを生成し、fitメソッドで学習、predictメソッドでテストデータセットに対する予測を実行します。max_depth=3とすることにより木の深さを3に設定します。
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
#Irisデータセットを読み込む
iris=load_iris()
x,y=iris.data,iris.target
#学習データセットとテストデータセットに分割する
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=1230)
#決定木をインスタンス化する
tree=DecisionTreeClassifier(max_depth=3)
#学習
tree.fit(x_train,y_train)それでは決定木を描画してみます。tree.pngを出力します。
from pydotplus import graph_from_dot_data
from sklearn.tree import export_graphviz
#dot形式のデータ抽出
dot_data=export_graphviz(tree,filled=True,rounded=True,
class_names=['Setosa','Versicolor','Virginical'],
feature_names=['Sepal Length','Sepal Width','Petal Length','Petal Width'],
out_file=None)
#決定木のプロット出力
graph=graph_from_dot_data(dot_data)
graph.write_png('tree.png')True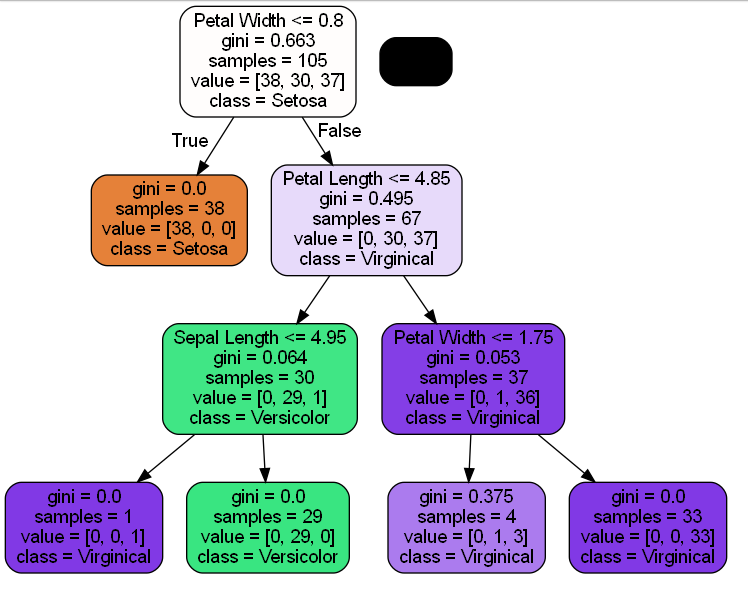
獲得した決定木について予測を行うには、predictメソッドを使用します。
tree.predict(x_test)array([0, 2, 2, 2, 1, 1, 0, 2, 2, 1, 0, 2, 1, 0, 0, 2, 1, 0, 1, 1, 1, 0,
0, 1, 1, 1, 1, 0, 2, 2, 0, 2, 1, 1, 1, 2, 2, 0, 2, 0, 1, 1, 2, 2,
1])ランダムフォレスト
ランダムフォレストはデータのサンプル特徴量(説明変数)をランダムに選択して決定木を構築する処理を繰り返し、各木の推定結果や多数決や平均値により分類・回帰を行う手法です。ランダムに選択されたサンプルと特徴量(説明変数)のデータをブートストラップデータと呼びます。
ランダムフォレストは決定木のアンサンブル(集合)であり、このように複数の学習器を用いた学習方法をアンサンブル学習といいます。
scikit-learnでランダムフォレストを実行するには、ensembleモジュールのRandomForestClassifireクラスを使用します。RandomForestClassifireクラスをインスタンス化する際にパラメータn_estimatorsには決定木の個数を指定します。
from sklearn.ensemble import RandomForestClassifier
#ランダムフォレストをインスタンス化
forest=RandomForestClassifier(n_estimators=100,random_state=1230)
#学習
forest.fit(x_train,y_train)
#予測
forest.predict(x_test)array([0, 1, 2, 2, 1, 1, 0, 2, 1, 1, 0, 2, 1, 0, 0, 2, 1, 0, 1, 1, 1, 0,
0, 1, 1, 1, 1, 0, 2, 2, 0, 2, 1, 1, 1, 2, 2, 0, 2, 0, 1, 1, 2, 2,
1])回帰
回帰とはある値(目的変数)を別の単一または複数の値(説明変数、特徴量)で説明するタスクです。
下記は回帰の例です。
- 賃貸住宅の家賃を物件の広さと居住地域で説明する(説明変数=物件の広さ、居住地域。目的変数=家賃)
線形回帰では、説明変数が1変数の場合は単回帰。2変数以上の場合は重回帰と呼ばれます。
scikit-learnで線形回帰を実行するには、liner_modelのLinerRegressionクラスセットを用いて実行できます。
下記のサンプルではBostonデータセット(米国ボストン市郊外の地域別の住宅価格と特徴量を記録したデータセット)を使用しています。
from sklearn.linear_model import LinearRegression
#from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
#Bostonデータセット読み込み(データセットが削除されているため直接指定)
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
x,y=data, target
#学習データとテストデータを分割
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=3,random_state=1230)
#線形回帰をインスタンス化
lr=LinearRegression()
#学習
lr.fit(x_train,y_train)
#テストデータを予測
y_pred=lr.predict(x_test)
y_predarray([18.7200232 , 29.93622642, 25.51785529])横軸を予測値、縦軸を実績値とする散布図をプロットしてみます。
import matplotlib.pyplot as plt
#横軸を予測値、縦軸を実績値とする散布図をプロット
fig,ax=plt.subplots()
ax.scatter(y_pred,y_test)
ax.plot((0,50),(0,50),linestyle='dashed',color='red')
ax.set_xlabel('predicted value')
ax.set_ylabel('actual value')
plt.show()
次元削減
次元削減とは、データが持っている情報をなるべく損ねることなく次元を削減してデータを圧縮するタスクです。
データの量を節約できるので計算を高速化でき、またデータが解釈しやすくなるというメリットがあります。 次元削減を用いることで、データセットの次元数を減らすことができます。
主成分分析
主成分分析は高次元のデータに対して分散が大きくなる方向(データが散らばる方向)を探して、元の次元と同じかそれよりも低い次元にデータを変換する手法です。scikit-learnで主成分分析を実行するには、decompositionモジュールのPCAクラスを使用します。
下記サンプルでは、2次元のデータを50個生成して主成分分析を実行します。
- x軸の値は、0以上1未満の一様乱数
- y軸の値は、x軸の値を2倍した後に、0以上1未満の一様乱数を0.5倍して足し合わせる
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1230)
#0以上1未満の一様乱数を50個生成
x=np.random.random(size=50)
#x軸の値を2倍した後に、0以上1未満の一様乱数を0.5倍して足し合わせる
y=2*x + 0.5*np.random.rand(50)
#散布図プロット
fig,ax=plt.subplots()
ax.scatter(x,y)
plt.show()50個の2次元データ
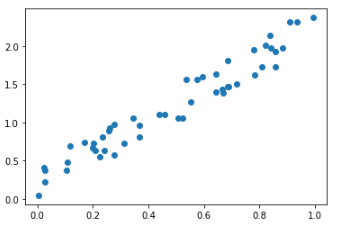
次に主成分分析を実行します。
PCAクラスをインスタンス化し、fitメソッドにデータの座標を表すNumpy配列を指定します。
今回の例では50×2の行列になります。
PCAクラスのインスタンス化を行う際に引数n_componentsに2を指定しています。
この2変数を主成分と呼び、1番目は第1主成分、2番目は第2主成分と呼びます。
from sklearn.decomposition import PCA
#主成分のクラスをインスタンス化
pca=PCA(n_components=2)
#主成分分析を実行
x_pca=pca.fit_transform(np.hstack((x[:,np.newaxis],y[:,np.newaxis])))
#主成分分析の結果を座標にプロット
fig,ax=plt.subplots()
ax.scatter(x_pca[:,0],x_pca[:,1])
ax.set_xlabel('pc1')
ax.set_xlabel('pc2')
ax.set_xlim(-1.1,1.1)
ax.set_ylim(-1.1,1.1)
plt.show()第一主成分と第二主成分の散布図

モデルの評価
分類と回帰のそれぞれに対して評価指標がありますが、ここでは分類の代表的な指標を見てみます。
分類ではデータのクラスをどの程度正確に当てられたかが重要です。下記の2つの観点で見てみます。
- カテゴリの分類精度
- 予測確率の正確さ
カテゴリの分類精度
データのカテゴリがどの程度当てられたかを定量化する指標として、適合率(precision)、再現率(recall)、F値(F-Value)、正解率(accuracy)などがあります。これらは混同行列から計算します。
| 実績 | |||
| 正例 | 負例 | ||
| 予測 | 正例と予測 | tp(真陽性) 正例と予測して実際に正例 | fp(偽陰性) 正例と予測したが実際は負例 |
| 負例と予測 | fn(偽陽性) 負例と予測したが実際は正例 | tn(真陰性) 負例と予測して実際に負例 |
適合率
正例と予測したデータのうち、実際に正例の割合を表す。
適合率=tp / (tp + fp)
再現率
実際の正例のうち、正例と予測したものの割合を表す。
再現率=tp / (tp + fn)
F値
適合率と再現率の調和平均
F値=2/(1/適合率 + 1/再現率)= 2 * 適合率 * 再現率/(適合率 + 再現率)
正解率
正例か負例かを問わず、予測と実績が一致した割合を表す。
正解率=(tp + tn) / (tp + fp + fn + tn)
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
iris=load_iris()
x,y=iris.data[:100,:], iris.target[:100]
#学習データとテストデータに分割
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=1230)
#SVMのインスタンス化
svc=SVC()
#SVMで学習
svc.fit(x_train,y_train)
#テストデータの予測
y_pred=svc.predict(x_test)classification_report関数を用いて、適合率、再現率、F値を出力します。
from sklearn.metrics import classification_report
#適合率、再現率、F値を出力
print(classification_report(y_test,y_pred)) precision recall f1-score support
0 1.00 1.00 1.00 13
1 1.00 1.00 1.00 17
accuracy 1.00 30
macro avg 1.00 1.00 1.00 30
weighted avg 1.00 1.00 1.00 30交差検証
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
scv=SVC()
#10分割の交差検証を実行
cross_val_score(svc,x,y,cv=10,scoring='precision')array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])クラスタリング
クラスタリングとは、ある基準を設定してデータ間の類似性を計算し、データをクラスタ(グループ)にまとめるタスクです。クラスタリングは教師なし学習の典型的なタスクです。
クラスタリングのアルゴリズムとして、k-meansと階層的クラスタリングの2つについて説明します。
この記事は役に立ちましたか?
もし参考になりましたら、下記のボタンで教えてください。

コメント