Numpyは、Pythonのサードパーティー製パッケージで配列や行列を効率よく扱えるようになっています。
Contents
Numpyでデータを扱う
import numpy as np1次元配列
a = np.array([1,2,3])入力・出力結果は下記となります。
a
array([1, 2, 3])
print(a)
[1 2 3]
type(a)
numpy.ndarray
a.shape
(3,) #1次元配列で3要素2次元配列
b = np.array([[1,2,3],[4,5,6]])入力・出力結果は下記となります。
b
array([[1, 2, 3],
[4, 5, 6]])
print(b)
array([[1, 2, 3],
[4, 5, 6]])
b.shape
(2, 3) #2×3行列変形(reshape)
次元の変換を行います。
c1=np.array([0,1,2,3,4,5])
c1array([0, 1, 2, 3, 4, 5])次元を変換する
c2=c1.reshape((2,3))
c2array([[0, 1, 2],
[3, 4, 5]])次元を元に戻す(ravel)
ravelは参照を返す
c3=c2.ravel()
c3array([0, 1, 2, 3, 4, 5])次元を元に戻す(flatten)
flattenはコピーを返す
c4=c2.flatten()
c4array([0, 1, 2, 3, 4, 5])データ型(dtype)
dtype属性を使って配列要素のデータ型を確認します。
a.dtypedtype('int32')データ型を指定して配列を作成することができます。
d=np.array([1,2],dtype=np.int16)
d.dtypedtype('int16')Numpy配列は整数以外にも浮動小数点や真偽値を扱うことができます。
astypeメソッドを使ってデータ型を変換することができます。
d.astype(np.float16)array([1., 2.], dtype=float16)インデックスとスライス
Numpy配列では、インデックスとスライスという方法を使って要素を取り出すことができます。
a = np.array([1,2,3])
aarray([1, 2, 3])インデックス値0を指定すると先頭のデータが取得できます。
a[0]1スライス位置を指定することで範囲指定が可能です。
a[1:]array([2, 3])負のインデックスも使用できます。
a[-1]32次元配列の場合、行方向の配列が取得できます。
b = np.array([[1,2,3],[4,5,6]])
barray([[1, 2, 3],
[4, 5, 6]])b[0]array([1, 2, 3])2つの値をカンマで区切って渡すと、行のインデックス値と列のインデックス値で示される値が取得できます。
b[1,0]4行または列をスライスの範囲で指定できます。
[行:列]なので[:,2]は行方向はすべて、列方向は2の区切り以降、つまり3番目の値を取得します。
b[:,2]array([3, 6])b[:,1]array([2, 5])その逆、[1, :]は行方向は2番目、列はすべてです。
b[1, :]array([4, 5, 6])行または列に対して個別に範囲指定も行えます。
b
array([[1, 2, 3],
[4, 5, 6]])b[0,1:]array([2, 3])すべての行に対してインデックス値の0と2の列を取得します。
b
array([[1, 2, 3],
[4, 5, 6]])b[:,[0,2]]array([[1, 3],
[4, 6]])データ再代入
a = np.array([1,2,3])
aarray([1, 2, 3])インデックス値[2]の値である3を5に置き換えます。
a[2]=5
aarray([1, 2, 5])2次元配列の置き換えもやってみましょう。
b = np.array([[1,2,3],[4,5,6]])
barray([[1, 2, 3],
[4, 5, 6]])2行目の3番目の値を6から8に置き換えます。
b[1,2]=8
barray([[1, 2, 3],
[4, 5, 8]])次にすべての行に対して、同じ列の値を変更します。
b[:,2]=9
barray([[1, 2, 9],
[4, 5, 9]])深いコピー(copy)
配列をコピーします。
a = np.array([1,2,3])
aarray([1, 2, 3])aをa1にコピー
a1 = a
a1array([1, 2, 3])a1の配列を変更します。
a1[1]=4
a1array([1, 4, 3])ここでaの配列を確認すると、こちらも変更されていることが分かります。
aarray([1, 4, 3])それでは、次にcopyメソッドを使ってデータをコピーしてみます。
a2 = a.copy()
a2array([1, 4, 3])a2の配列を変更します。
a2[2] = 5
a2array([1, 4, 5])ここでaの配列を確認すると、値はそのままであることが分かります。
aarray([1, 4, 3])数列を返す(arange)
arange関数を使うと、Numpy配列(ndarray)が生成されます。
np.arange(10)array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])引数として下記にように2つの整数を指定した場合も同じ結果となります。
np.arange(0,10)array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])引数を3つ指定すると(先頭インデックス, 末尾インデックス, 間隔)となります。
np.arange(0,10,2)array([0, 2, 4, 6, 8])乱数
np.random.random関数は、行と列のタプルを渡すと0以上1未満の範囲の乱数2次元配列を生成します。
f = np.random.random((3,2))
farray([[0.42993696, 0.35811396],
[0.64468516, 0.66031175],
[0.93312053, 0.47026511]])乱数を使用すると毎回違った値で生成されますが、乱数のシード値を固定することで毎回同じ値を生成することが可能です。
np.random.seed(1230)
np.random.random((3,2))array([[0.27702631, 0.36855193],
[0.64431478, 0.78019793],
[0.50860458, 0.52375554]])np.random.rand関数は、np.random.random関数と同様に0-1範囲の乱数配列を生成します。
np.random.seed(1230)
np.random.rand(3,2)array([[0.27702631, 0.36855193],
[0.64431478, 0.78019793],
[0.50860458, 0.52375554]])ある範囲内の任意の整数を生成するには、np.randoom.randint関数を使用します。
np.random.seed(1230)
np.random.randint(1,10)21以上10未満の整数の中から1つの整数が出力されました。
第三引数を指定すると行と列の二次元配列を生成します。
np.random.seed(1230)
np.random.randint(1,10,(3,2))array([[2, 7],
[4, 2],
[9, 9]])np.random.uniform関数は、第一引数以上かつ第二引数未満のランダムな小数値を、第三引数としてタプルで渡した行と列の二次元配列で生成します。第一・第二引数を省略すると0.0と1.0がデフォルトで設定されます。
np.randoom.randint関数との違いは、戻り値となるndarrayの要素が小数値になることです。
np.random.seed(1230)
np.random.uniform(0.0,5.0,(2,3))array([[1.38513155, 1.84275963, 3.22157388],
[3.90098963, 2.54302288, 2.61877768]])デフォルトの場合
np.random.seed(1230)
np.random.uniform(size=(4,3))array([[0.27702631, 0.36855193, 0.64431478],
[0.78019793, 0.50860458, 0.52375554],
[0.84079088, 0.36703687, 0.67039217],
[0.83824478, 0.68695113, 0.10454645]])np.random.randn関数は、np.random.rand関数と同様に引数に形状を渡します。
出力される乱数が標準正規分布に従い、平均0、分数1の分布で出力されます。
np.random.seed(1230)
np.random.randn(4,2)array([[-0.82415727, -1.39800747],
[ 1.20783861, 0.62209225],
[ 3.24895652, 1.17681599],
[-0.40637194, 1.04155078]])同じ要素の数列を作る
zeros関数に整数で引数を渡すと、指定した要素数の0.0が入った数列を取得します。
np.zeros(3)array([0., 0., 0.])2次元配列の場合
np.zeros((2,3))array([[0., 0., 0.],
[0., 0., 0.]])ones関数に整数で引数を渡すと、指定した要素数の1.0が入った数列を取得します。
np.ones(3)array([1., 1., 1.])2次元配列の場合
np.ones((2,3))array([[1., 1., 1.],
[1., 1., 1.]])単位行列
eye関数を使って指定する対角要素を持った単位行列を作ることができます。
単位行列とは、数学で、正方行列の対角成分が1で、それ以外が零である行列。
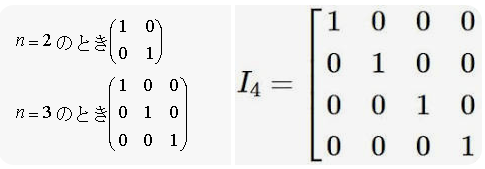
np.eye(3)array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])指定値で埋める
指定の値で配列を作ることができます。
full関数を使用します。第一引数が要素数、第二引数が指定値
np.full(3,3.14)array([3.14, 3.14, 3.14])次に行と列を指定します。第二引数には円周率を表すnp.piを用います。
np.full((2,4),np.pi)array([[3.14159265, 3.14159265, 3.14159265, 3.14159265],
[3.14159265, 3.14159265, 3.14159265, 3.14159265]])np.nanはNumpyの欠損値の穴埋めなどに使われます。
np.nannannp.array([1,2,np.nan])array([ 1., 2., nan])範囲指定で均等割りデータを作る
linspace関数を使って、0から2までを等間隔に区切った5つの要素の配列を作ります。
np.linspace(0,2,5)array([0. , 0.5, 1. , 1.5, 2. ])円周率np.piを20分割した場合
np.linspace(0,np.pi,21)array([0. , 0.15707963, 0.31415927, 0.4712389 , 0.62831853,
0.78539816, 0.9424778 , 1.09955743, 1.25663706, 1.41371669,
1.57079633, 1.72787596, 1.88495559, 2.04203522, 2.19911486,
2.35619449, 2.51327412, 2.67035376, 2.82743339, 2.98451302,
3.14159265])要素間の差分
np.diff関数は、要素間の差分を返します。
np.diff(np.array([3,3,6,2,4]))array([ 0, 3, -4, 2])連結
concatenate関数を使って、連結を行います。
a1 = np.array([1,2,3])
a2 = np.array([4,5,6])
print(a1)
print(a2)[1 2 3]
[4 5 6]2つの配列を連結します。
np.concatenate([a1,a2])array([1, 2, 3, 4, 5, 6])2次元配列の連結を行います。
まず連結する配列b,b1を生成します。
b=np.array([[1,2,3],[4,5,6]])
barray([[1, 2, 3],
[4, 5, 6]])b1=np.array([[10],[20]])
b1array([[10],
[20]])連結を行います。カラムの列方向を増やす場合は、axis=1と指定します。
np.concatenate([b,b1],axis=1)array([[ 1, 2, 3, 10],
[ 4, 5, 6, 20]])hstack関数を使うと同様の結果となります。
hstack関数は列方向に連結します。
np.hstack([b,b1])array([[ 1, 2, 3, 10],
[ 4, 5, 6, 20]])b=np.array([[1,2,3],[4,5,6]])
barray([[1, 2, 3],
[4, 5, 6]])ここでb2という1次元配列を生成します。
b2 = np.array([10,20,30])
b2array([10, 20, 30])vstack関数は行方向に連結します。
b3 = np.vstack([b,b2])
b3array([[ 1, 2, 3],
[ 4, 5, 6],
[10, 20, 30]])分割
hsplit関数を使って、列の途中で分割することができます。
第一引数が対象の配列、第二引数が分割する部分です。
第二引数に[2]を指定すると、1つ目の配列が2列となり、残り1列がもうひとつの配列となります。
first,second = np.hsplit(b3,[2])firstarray([[ 1, 2],
[ 4, 5],
[10, 20]])secondarray([[ 3],
[ 6],
[30]])転置
2次元配列の行と列を入れ替えることを転置といいます。
転置にはTを使います。
b=np.array([[1,2,3],[4,5,6]])
barray([[1, 2, 3],
[4, 5, 6]])b.Tarray([[1, 4],
[2, 5],
[3, 6]])次元追加
np.newaxis関数は次元を1つ増やします。
a = np.array([1,2,3])
aarray([1, 2, 3])行方向を増やします。
a[np.newaxis,:]array([[1, 2, 3]])列方向を増やします。
a[:,np.newaxis]array([[1],
[2],
[3]])np.newaxis関数は、np.reshape関数と違って要素数を指定する必要がありません。
グリッドデータの生成
meshgrid関数は2次元上の点に対応する等高線やヒートマップなどを描くときに使用します。
x座標、y座標の配列から組み合わせて座標データを生成します。
m = np.arange(0,4)
marray([0, 1, 2, 3])n = np.arange(4,7)
narray([4, 5, 6])mとn方向にグリッドデータを生成します。
xx, yy = np.meshgrid(m,n)
xxarray([[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3]])yyarray([[4, 4, 4, 4],
[5, 5, 5, 5],
[6, 6, 6, 6]])この記事は役に立ちましたか?
もし参考になりましたら、下記のボタンで教えてください。

コメント